Generating Language

Synthesis

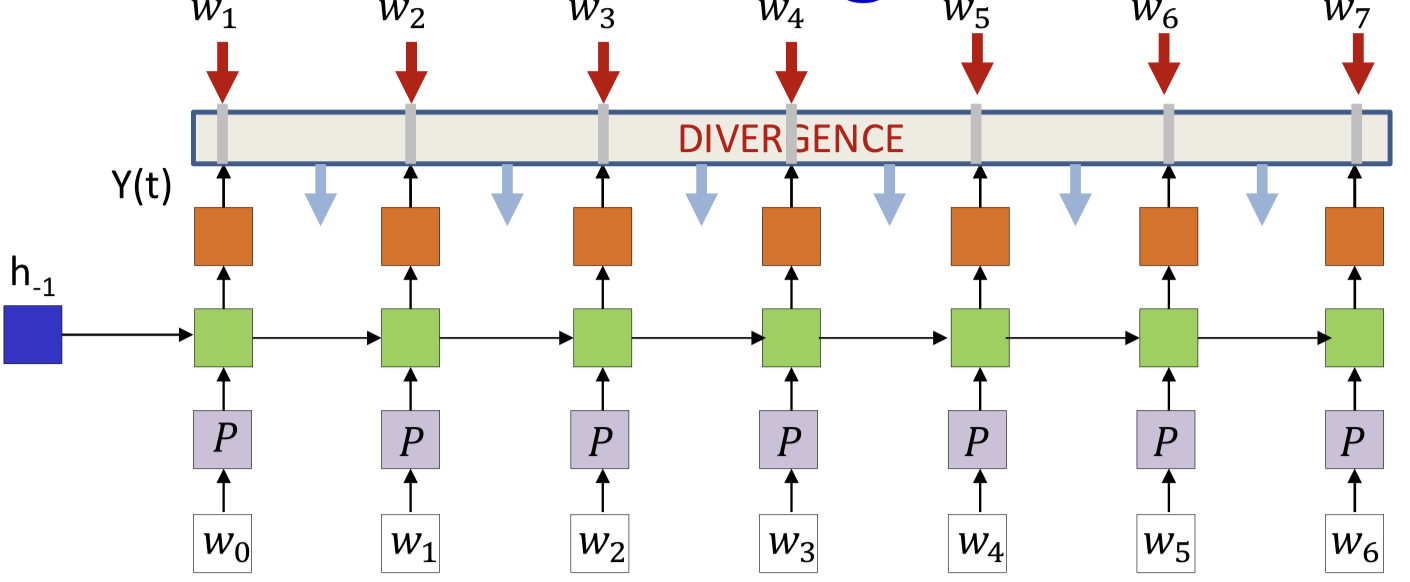
• Input: symbols as one-hot vectors
  • Dimensionality of the vector is the size of the 「vocabulary」
  • Projected down to lower-dimensional “embeddings”
• The hidden units are (one or more layers of) LSTM units
• Output at each time: A probability distribution that ideally assigns peak probability to the next word in the sequence
• Divergence

$\operatorname{Div}(\mathbf{Y}_{\text {target}}(1 \ldots T), \mathbf{Y}(1 \ldots T))=\sum\_{t}\operatorname{Xent}(\mathbf{Y}\_{\text {target}}(t), \mathbf{Y}(t))=-\sum\_{t} \log Y(t, w\_{t+1})$

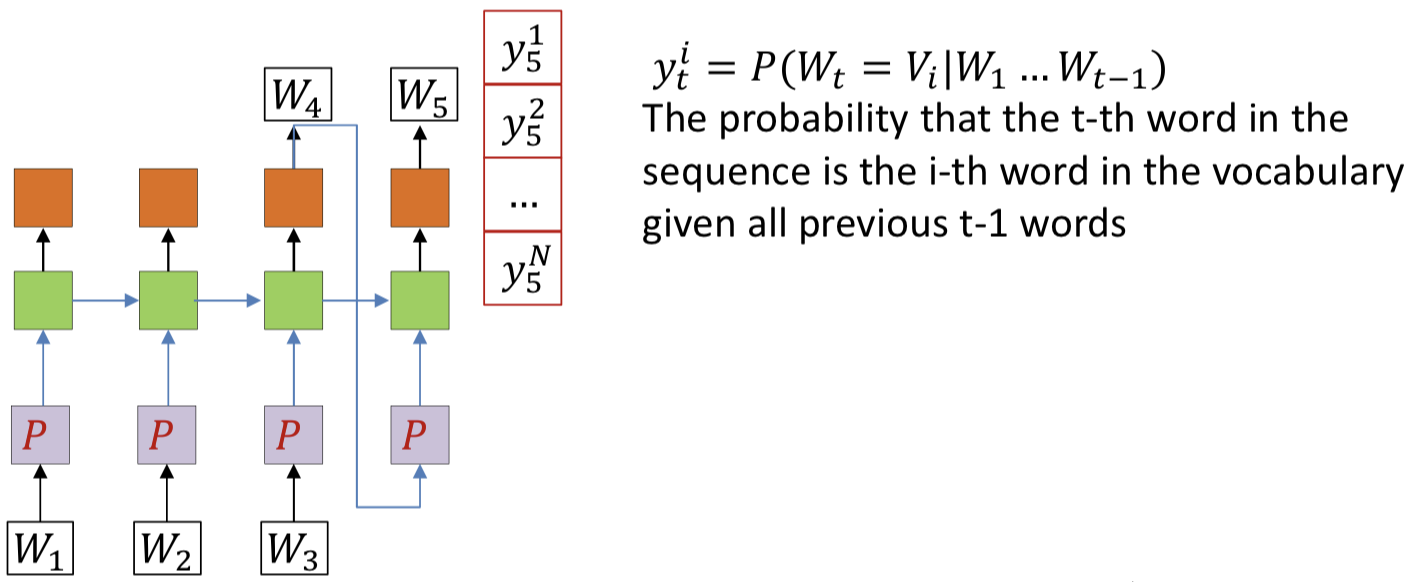
• Feed the drawn word as the next word in the series
• And draw the next word from the output probability distribution

Beginnings and ends

• A sequence of words by itself does not indicate if it is a complete sentence or not
• To make it explicit, we will add two additional symbols (in addition to the words) to the base vocabulary
  • <sos>: Indicates start of a sentence
  • <eos> : Indicates end of a sentence
• When do we stop?
  • Continue this process until we draw an <eos>
  • Or we decide to terminate generation based on some other criterion

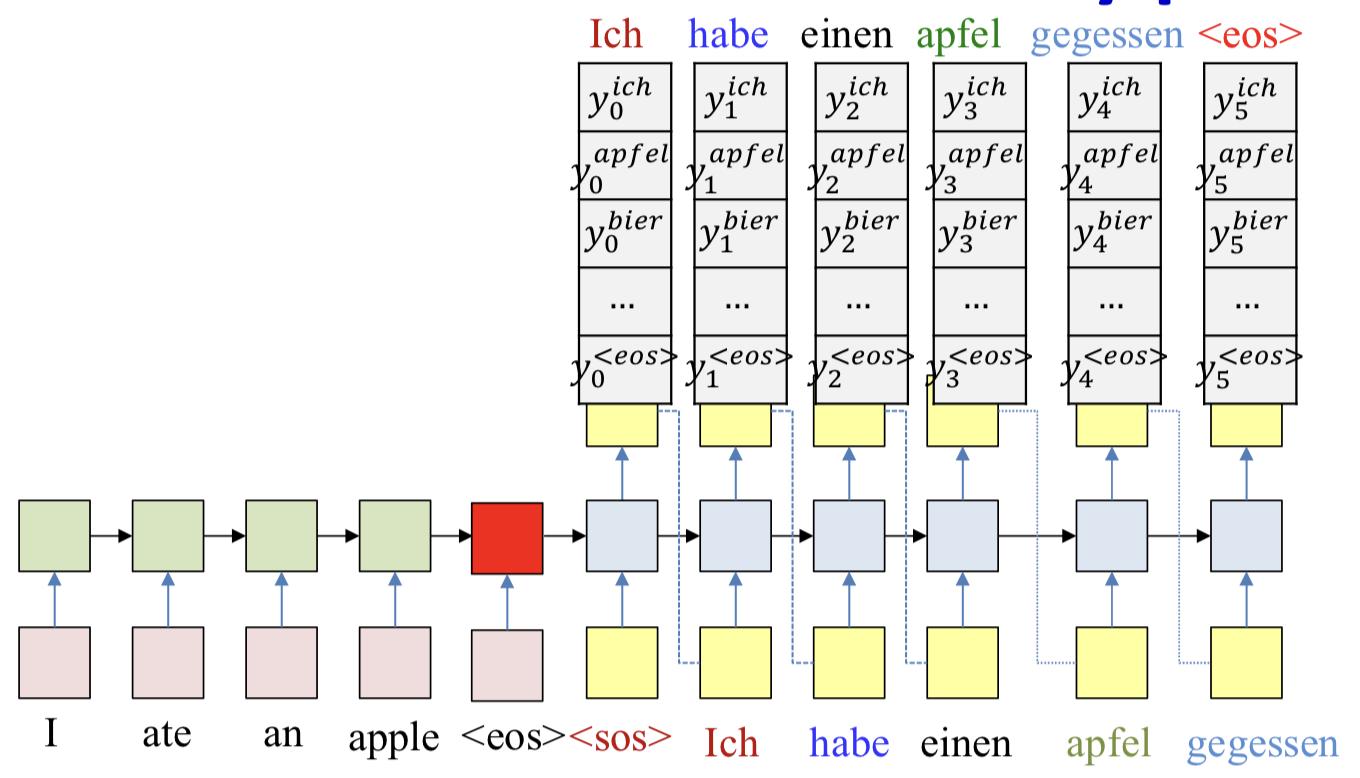
Delayed sequence to sequence

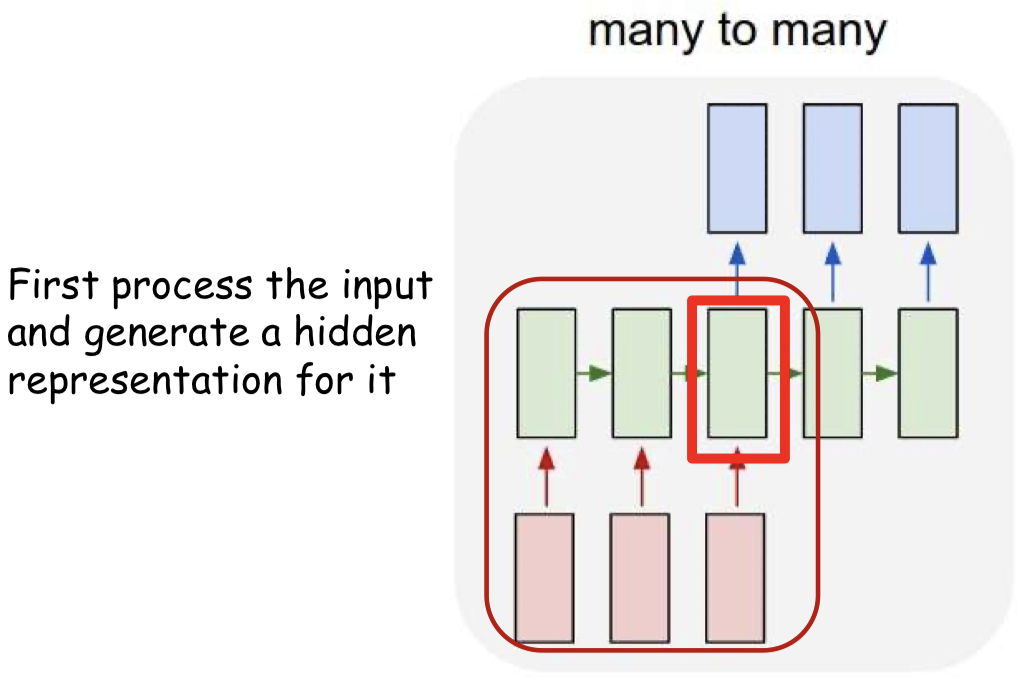
Pseudocode

• Problem: Each word that is output depends only on current hidden state, and not on previous outputs
• The input sequence feeds into a recurrent structure
• The input sequence is terminated by an explicit <eos> symbol
  • The hidden activation at the <eos> “stores” all information about the sentence
• Subsequently a second RNN uses the hidden activation as initial state to produce a sequence of outputs
  • The output at each time becomes the input at the next time
  • Output production continues until an <eos> is produced

Autoencoder

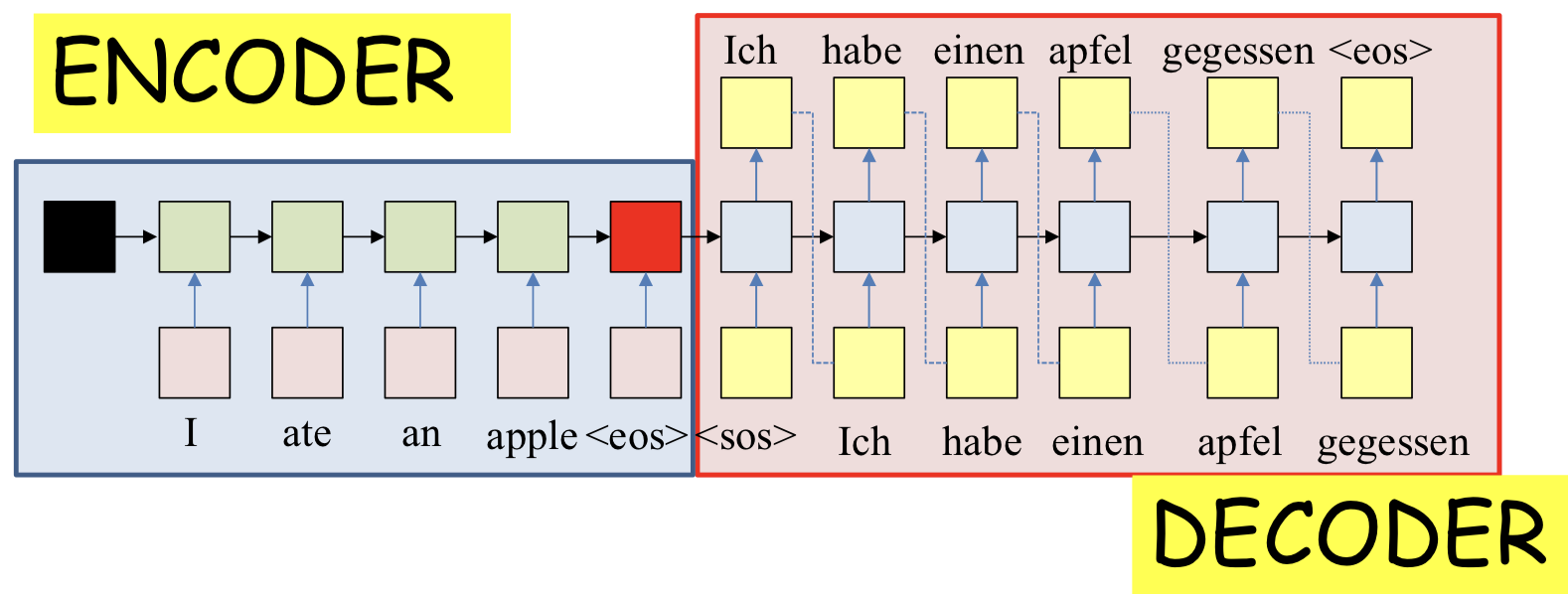
• The recurrent structure that extracts the hidden representation from the input sequence is the encoder
• The recurrent structure that utilizes this representation to produce the output sequence is the decoder

Generating output

• At each time the network produces a probability distribution over words, given the entire input and previous outputs
• At each time a word is drawn from the output distribution

$P\left(O_{1}, \ldots, O_{L} \mid W_{1}^{i n}, \ldots, W_{N}^{i n}\right)=y_{1}^{O_{1}} y_{1}^{O_{2}} \ldots y_{1}^{O_{L}}$

• The objective of drawing: Produce the most likely output (that ends in an <eos>)

$\underset{O_{1}, \ldots, O_{L}}{\operatorname{argmax}} y_{1}^{O_{1}} y_{1}^{O_{2}} \ldots y_{1}^{O_{L}}$

• How to draw words?
  • Greedy answer
    • Select the most probable word at each time
    • Not good, making a poor choice at any time commits us to a poor future
  • Randomly draw a word at each time according to the output probability distribution
    • Not guaranteed to give you the most likely output
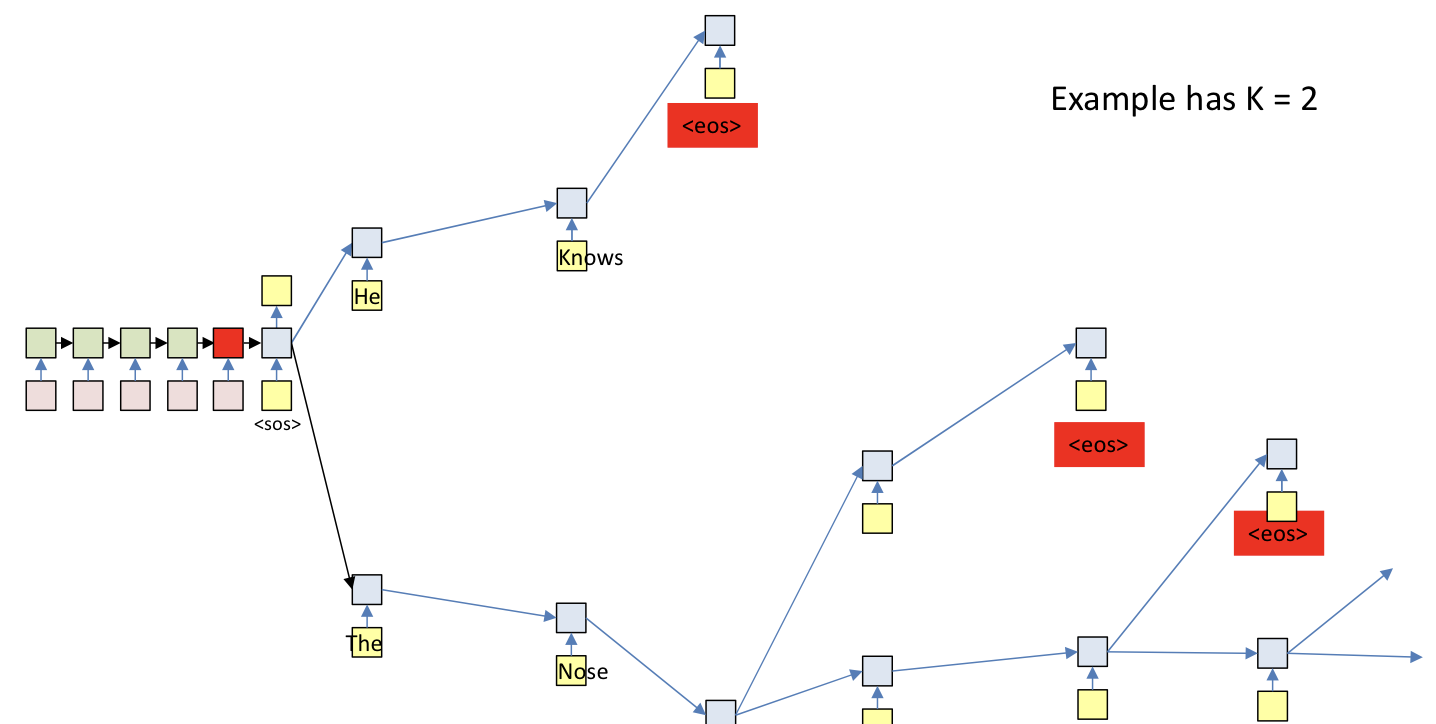
  • Beam search
    • Search multiple choices and prune
    • At each time, retain only the top K scoring forks
    • Terminate: When the current most likely path overall ends in <eos>

Train

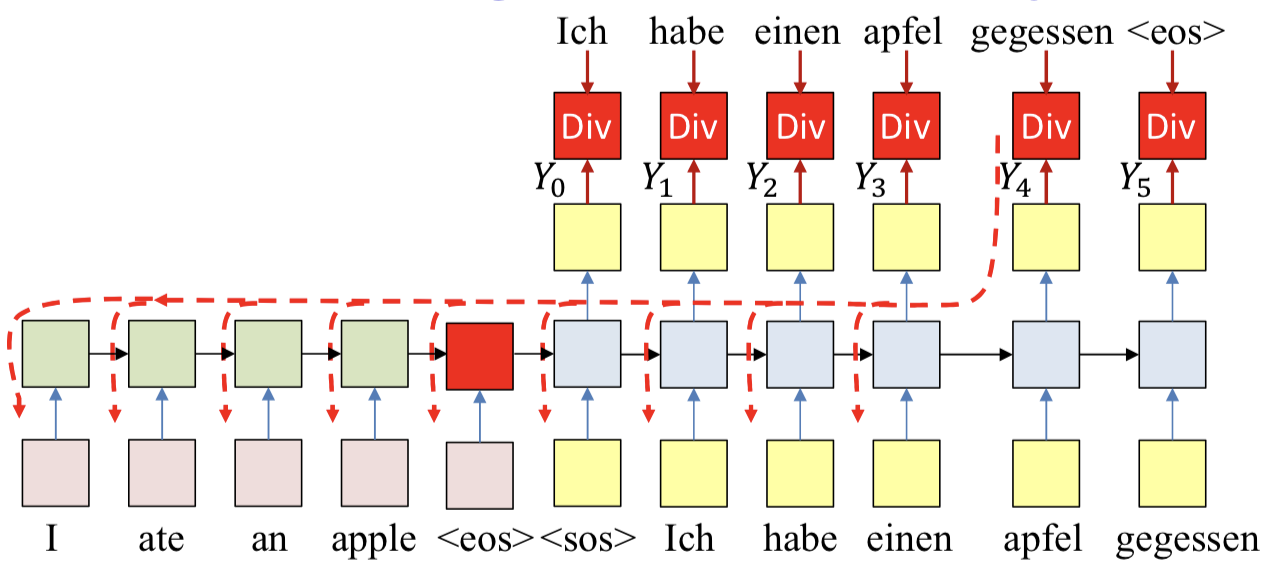
• In practice, if we apply SGD, we may randomly sample words from the output to actually use for the backprop and update
  • Randomly select training instance: (input, output)
  • Forward pass
  • Randomly select a single output $y(t)$ and corresponding desired output $d(t)$ for backprop
• Trick
  • The input sequence is fed in reverse order
    • This happens both for training and during actual decode
• Problem
  • All the information about the input sequence is embedded into a single vector
  • In reality: All hidden values carry information

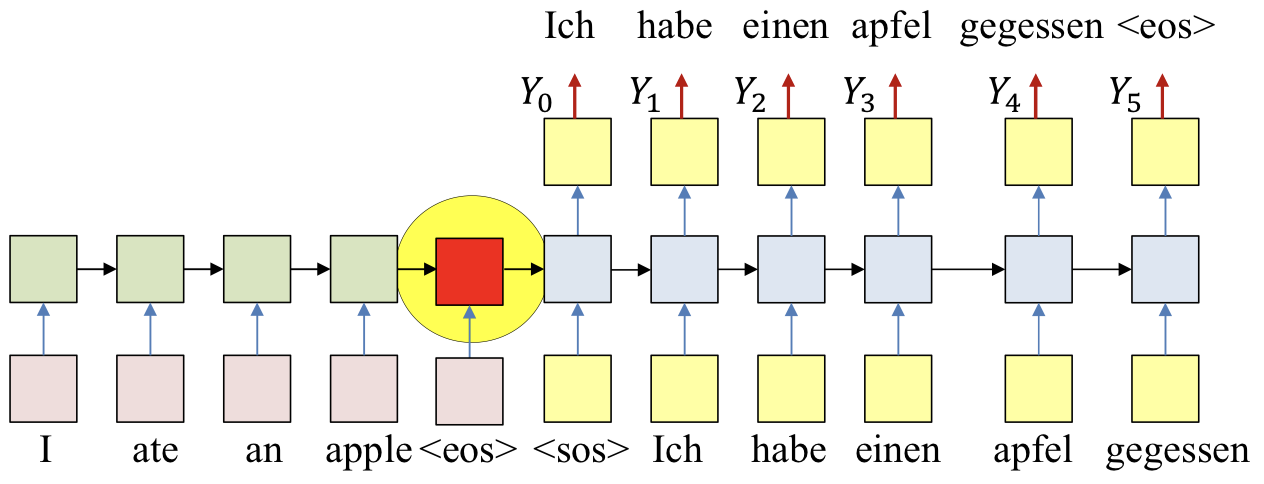
Attention model

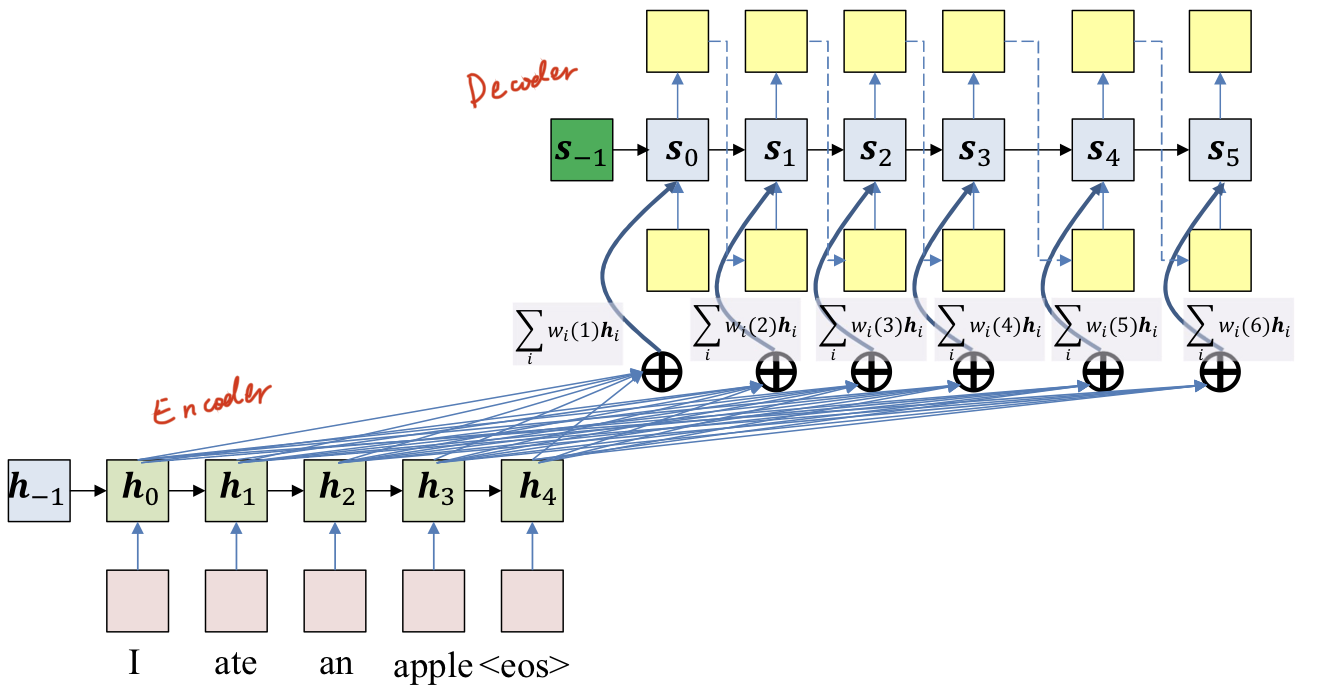
• Compute a weighted combination of all the hidden outputs into a single vector
  • Weights vary by output time
• Require a time-varying weight that specifies relationship of output time to input time
  • Weights are functions of current output state

$e_{i}(t)=g\left(\boldsymbol{h}_{i}, \boldsymbol{s}_{t-1}\right)$

$w_{i}(t)=\frac{\exp \left(e_{i}(t)\right)}{\sum_{j} \exp \left(e_{j}(t)\right)}$

Attention weight

• Typical option for $g()$
  • Inner product
    • $g\left(\boldsymbol{h}\_{i}, \boldsymbol{s}\_{t-1}\right)=\boldsymbol{h}\_{i}^{T} \boldsymbol{s}\_{t-1}$
  • Project to the same demension
    • $g\left(\boldsymbol{h}_{i}, \boldsymbol{s}\_{t-1}\right)=\boldsymbol{h}\_{i}^{T} \boldsymbol{W}\_{g} \boldsymbol{s}\_{t-1}$
  • Non-linear activation
    • $g\left(\boldsymbol{h}\_{i}, \boldsymbol{s}\_{t-1}\right)=v\_{g}^{T} \boldsymbol{t} \boldsymbol{a} \boldsymbol{n} \boldsymbol{h}\left(\boldsymbol{W}\_{g}\left[\begin{array}{c}\boldsymbol{h}_{i} \\\\ \boldsymbol{s}\_{t-1}\end{array}\right]\right)$
  • MLP
    • $g\left(\boldsymbol{h}\_{i}, \boldsymbol{s}\_{t-1}\right)=\operatorname{MLP}\left(\left[\boldsymbol{h}\_{i}, \boldsymbol{s}\_{t-1}\right]\right)$

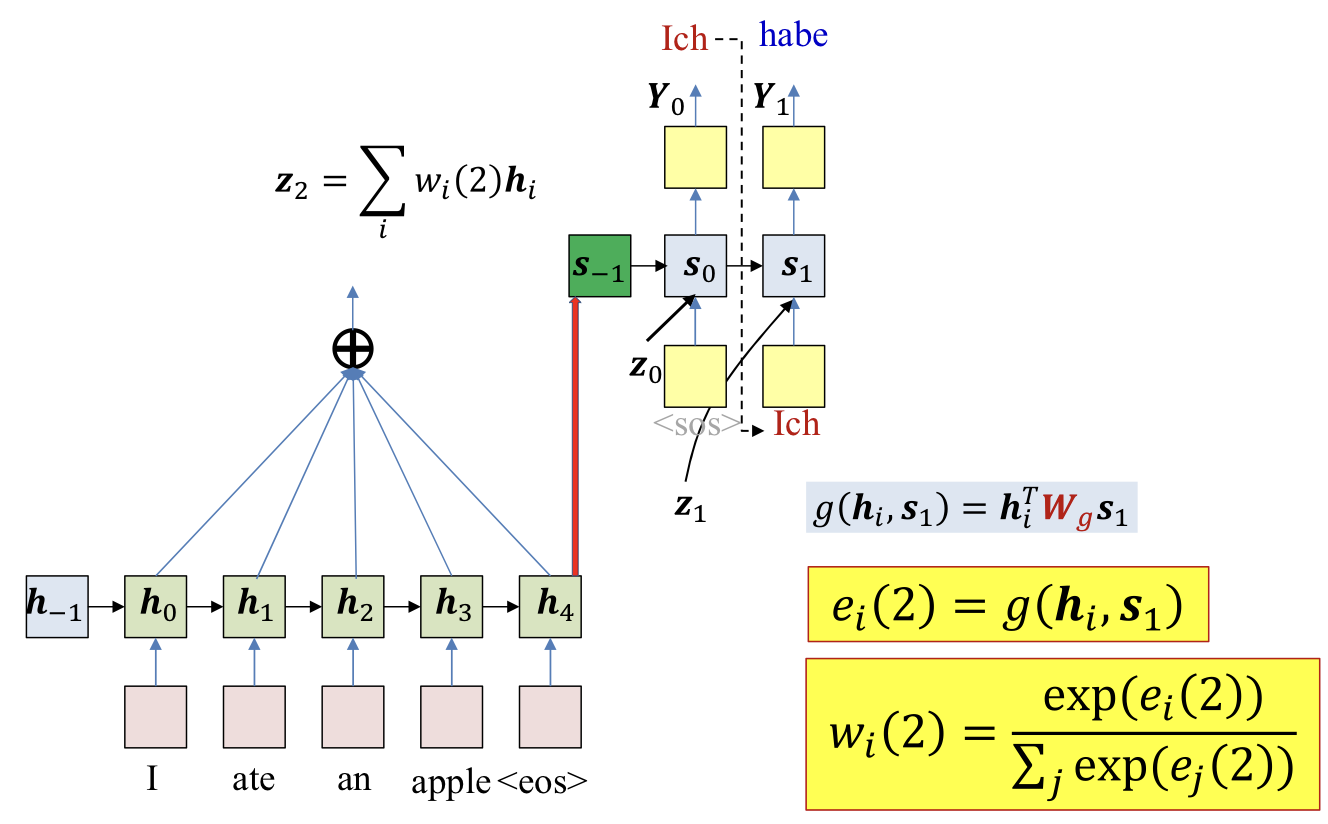
Pseudocode

Train

• Back propagation also updates parameters of the “attention” function
• Trick: Occasionally pass drawn output instead of ground truth, as input
  • Randomly select from output, force network to produce correct word even the prioir word is not correct

variants

• Bidirectional processing of input sequence
  • Neural Machine Translation by Jointly Learning to Align and Translate
• Local attention vs global attention
  • Effective Approaches to Attention-based Neural Machine Translation
• Multihead attention
  • Derive 「value」, and multiple 「keys」 from the encoder
    • $V_{i}, K_{i}^{l}, i=1 \ldots T, l=1 \ldots N_{\text {head}}$
  • Derive one or more 「queries」 from decoder
    • $Q_{j}^{l}, j=1 \ldots M, l=1 \ldots N_{\text {head}}$
  • Each query-key pair gives you one attention distribution
    • And one context vector
    • $a_{j, i}^{l}=$attention$\left(Q_{j}^{l}, K_{i}^{l}, i=1 \ldots T\right), \quad C_{j}^{l}=\sum_{i} a_{j, i}^{l} V_{i}$
  • Concatenate set of context vectors into one extended context vector
    • $C_{j}=\left[C_{j}^{1} C_{j}^{2} \ldots C_{j}^{N_{\text {head}}}\right]$
  • Each 「attender」 focuses on a different aspect of the input that’s important for the decode